Dear Editor,
The Court of Appeal (COA) ruled that 34 – not 33 – constitutes an absolute majority of 65. In my humble opinion both 33 and 34 are correct answers. The methodology the court used to rule out 33 is wrong.
This is a question of examining and solving Inequalities (a topic in 9th to 12 grade Math courses). It is not a question of dividing 65 by 2 = 32.5, then round to nearest whole number, 33, then add 1 = 34.
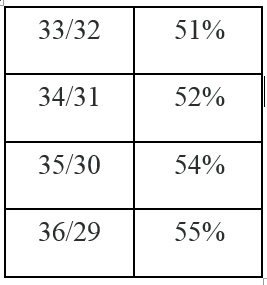
Think of a pie that is split into two unequal parts. Majority/minority parts. Each time the parts add up to 65. There are many majorities (with their percentage majorities) as follows:
How do the Justices know which majority the Constitution is talking about – which is a simple majority? And, which is an absolute majority? The 33/32 split works out to a 51% majority, 34/31 to a 52% majority etc.
Note: Each split of the pie must add up to 65. The methodology accepted by the court does not add up to 65 – and therefore the COA has committed a mistake by accepting an incorrect solution to an inequality math problem.
In all Inequality problems, you are dealing with solution sets. And, in the illustration, 33, 34, 35, 36 are all correct answers. The actual vote in the parliament is 33/32 – and because 33 is included in the solution set, it is a proper majority.
It is still a mystery to me as to what is the difference between a simple majority and an absolute majority as it relates to this Guyana math problem case. I have grave doubts as to whether the Justices of the COA have an answer to this latter question.
Yours faithfully,
Mike Persaud